Phương trình bậc nhất một ẩn lớp 8 là phần kiến thức quan trọng, tạo nền tảng để các bạn học tốt những chuyên đề toán học tiếp theo. Với bất kì môn học nào cũng vậy, kiến thức mới thì luôn khó nhưng có sự thú vị riêng. Nếu bạn đang loay hoay trong “ngã kẹt” về cách giải phương trình bậc nhất một ẩn thì cũng đừng quá lo lắng.
Ở bài viết này, gia sư Thành Tâm sẽ hướng dẫn các bạn một cách chi tiết về cách giải và bài tập phương trình bậc nhất 1 ẩn. Hãy cùng đọc và tham khảo nhé!
Giới thiệu về phương trình bậc nhất một ẩn
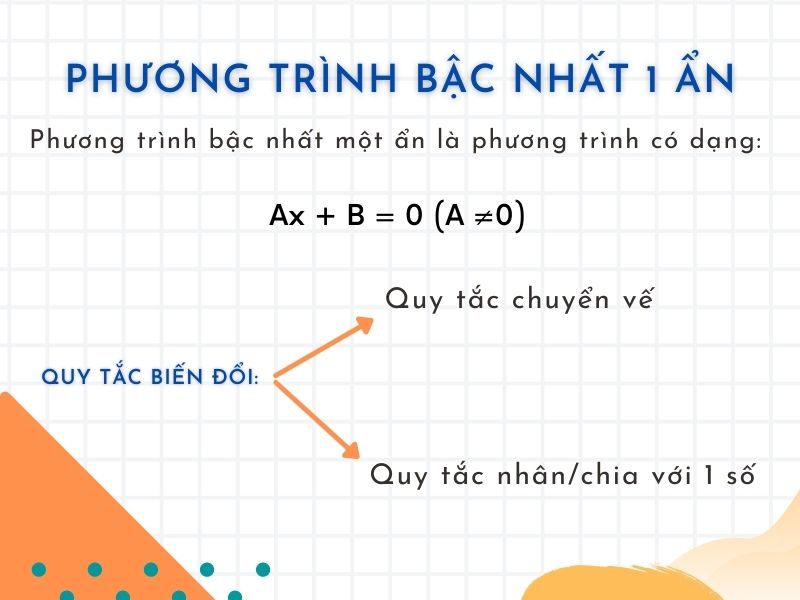
Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (a≠0), với a và b là hai số đã cho.
Ví dụ:
1/ 5x + 6 = 0
2/ 7x + 2 = 0
3/ 4y + 8 = 0
Quy tắc biến đổi phương trình bậc nhất một ẩn
Sau đây, gia sư Thành Tâm xin gửi đến các bạn hai quy tắc “vàng” trong cách biến đổi một phương trình. Cụ thể:
- Quy tắc chuyển vế
Khi chuyển vế một hạng tử từ vế này sang vế kia trong một phương trình thì phải ĐỔI DẤU hạng tử đó.
Ví dụ: 4x + 18 = 0
Vế trái: 4x + 18
Vế phải: 0
→ Khi chuyển số 18 từ vế trái sang vế phải thì các bạn phải đổi dấu thành -18. Khi đó phương trình trở thành: 4x = -18
- Quy tắc nhân hoặc chia với một số
Các bạn có thể nhân hai vế (trái và phải) của một phương trình với một số khác 0. Khi đó, ta được một phương trình với tương đương với phương trình đã cho.
Ví dụ: -2x/3 = 1
→ Các bạn nhân 2 vế của phương trình với 3 thì được: -2x = 6
Cách giải phương trình bậc nhất một ẩn
Vấn đề quan trọng nhất trong cách giải phương trình bậc nhất một ẩn đó chính là các bạn phải nắm vững quy tắc chuyển vế và nhân/chia hai vế của một phương trình cho một số khác 0.
Sau đây, gia sư lớp 8 của Thành Tâm sẽ lần lượt hướng dẫn các bước giải phương trình ax + b = 0 (a≠0). Cụ thể:
Cách giải phương trình bậc nhất 1 ẩn dạng cơ bản nhất
Bước 1: Chuyển phương trình về dạng ax = -b
Bước 2: Chia cả hai vế cho a, khi đó ta được phương trình: x = -b/a.
Bước 3: Kết luận nghiệm. Vậy nghiệm của phương trình là: x = -b/a
Lưu ý: Phương trình bậc nhất dạng ax + b = 0 (a≠0) chỉ có 1 nghiệm duy nhất x = -b/a
Ví dụ: Giải phương trình: 5x + 32 = 0
Ta có: 5x + 32 = 0 ⇔ 5x = -32 ⇔ x = -32/5
Vậy nghiệm của phương trình là x = -32/5.

Cách giải phương trình tích bậc nhất 1 ẩn dạng A(x).B(x) = 0
Phương trình có dạng: A(x). B(x) = 0, khi đó: A(x) = 0 hoặc B(x) = 0. Lúc này, các bạn đưa về giải phương trình bậc nhất 1 ẩn cơ bản như trên.
Ví dụ: Giải phương trình: (2x + 5).(3x + 7) = 0
Ta có: (2x + 5).(3x + 7) = 0
⇔ 2x + 5 = 0 hoặc 3x + 7 = 0
- 2x + 5 = 0 ⇔ 2x = -5 ⇔ x = -5/2
- 3x + 7 = 0 ⇔ 3x = -7 ⇔ x = -7/3
Vậy nghiệm của phương trình là: x = -5/2 hoặc x = -7/3
Cách giải phương trình bậc nhất chứa ẩn ở mẫu
Bước 1: Tìm điều kiện xác định ĐKXĐ (Mẫu số khác 0).
Bước 2: Quy đồng mẫu thức và bỏ mẫu.
Bước 3: Giải phương trình sau khi bỏ mẫu.
Bước 4: Kiểm tra các nghiệm vừa tìm được có thỏa mãn ĐKXĐ không, nghiệm nào thỏa mãn, nghiệm nào không thỏa mãn.
Bước 5: Kết luận nghiệm của phương trình.
Ví dụ: (2x – 5)/(x+5) = 3
- Điều kiện xác định: x + 5 ≠ 0 ⇔ x ≠ -5
Ta có: (2x – 5)/(x+5) = 3
⇔ (2x – 5)/(x+5) = 3.(x+5)/(x+5)
⇔ 2x – 5 = 3(x+5)
⇔ 2x – 5 = 3x + 15
⇔ x = -20 (thỏa mãn điều kiện)
Vậy nghiệm của phương trình là: x = -20
Cách giải và biện luận nghiệm phương trình bậc nhất một ẩn
Ta dùng các quy tắc chuyển vế và quy tắc nhân với một số để giải phương trình. Cách biện luận phương trình 1 ẩn cụ thể như sau:
Cho phương trình ax + b = 0 (a≠0) (1)
- Nếu a= 0, b=0 thì phương trình (1) có vô số nghiệm.
- Nếu a = 0, b ≠ 0 thì phương trình (1) vô nghiệm.
- Nếu a ≠ 0 thì phương trình có nghiệm duy nhất x = -b/a
Ví dụ: Giải và biện luận phương trình sau với m là tham số: (m-1)x + 2 – m = 0
→ Hướng dẫn giải:
Phương trình đã cho tương đương với (m-1)x = m=2
- Với m-1 = 0 ⇔ m = 1: Phương trình trở thành 0x = -1, suy ra phương trình vô nghiệm.
- Với m-1 ≠ 0 ⇔ m ≠ 1: Phương trình tương đương với x = (m-2)/(m-1)
Kết luận:
→ Nếu m = 1, phương trình vô nghiệm.
→ Nếu m ≠ 1, phương trình có nghiệm duy nhất x = (m-2)/(m-1)
Bài tập tự luyện:
Bài 1: Tìm m để phương trình sau vô nghiệm
a/ (m² – m)x = 2x + m² – 1
b/ m² (x – m) = x – 3m + 2
Bài 2: Giải và biện luận phương trình với m là tham số:
a/ (2m-4)x + 2 – m = 0
b/ (m+1)x = (3m² – 1) + m – 1
TÓM LẠI LÀ:
Gia sư dạy kèm lớp 8 của Thành Tâm hi vọng qua bài viết này, các bạn sẽ lần lượt giải đáp được những thắc mắc về cách giải phương trình bậc nhất một ẩn. Trong bất kỳ chuyên đề toán nào cũng vậy, điều quan trọng nhất là các bạn phải hiểu đúng bản chất của nó. Từ kiến thức cơ bản nền tảng, bạn sẽ làm được những bài toán dễ, áp dụng tư duy logic để giải quyết bài toán khó hơn.
Trong đề thi, số lượng phương trình bậc nhất 1 ẩn cơ bản nhất chỉ có một vài câu mà thôi. Các câu còn lại, các bạn phải tư duy biến đổi quy về phương trình cơ bản thì mới làm được. Hãy làm bài tập thật nhiều để có phương pháp học toán hiệu quả nhất bạn nhé!
Mọi chi tiết và thắc mắc vui lòng liên hệ về số hotline 0374771705 hoặc fanpage để được tư vấn và hướng dẫn.
TRUNG TÂM GIA SƯ THÀNH TÂM – NƠI CUNG CẤP GIA SƯ CHẤT LƯỢNG HÀNG ĐẦU TẠI HCM
Văn phòng đại diện: 35/52 Đường 44, Phường Hiệp Bình Chánh, Quận Thủ Đức
HOTLINE: 0374771705 (Cô Tâm)
>>> Xem thêm: [Tư vấn] Tìm gia sư lớp 7 dạy kèm các môn tận tâm, đúng yêu cầu!

Gia Sư Đà Nẵng: [Tư Vấn] Tìm Gia Sư Các Môn từ lớp 1-12!
Chi nhánh gia sư Đà Nẵng của Thành Tâm đã hoạt động hơn 6 năm, ...
Th11
[Chuẩn] Cách Học Tốt Môn Lịch Sử Lớp 12 Để Ôn Thi THPT
Môn Lịch Sử là một trong 3 môn xã hội được quy định trong kì ...
Th10
Kinh Nghiệm, Nội Dung Kiến Thức Ôn Thi Vào Lớp 10 Môn Văn 2023
Toán – Văn – Anh là bộ ba môn học mà Bộ GD-ĐT lựa chọn ...
Th10
Chia Đa Thức Cho Đơn Thức Lớp 8: Lý Thuyết & Bài Tập!
Chia đa thức cho đơn thức nằm ở phần chương 1 toán đại số của ...
Th10
[Tóm Tắt A-Z] Chương Trình Toán Lớp 10- Gia Sư Thành Tâm
Chương trình toán lớp 10 gồm những chuyên đề nào? Số lượng bài và tổng ...
Th9
[Đầy Đủ] Phương pháp luyện thi THPT quốc gia tổ hợp môn xã hội
Tổ hợp môn xã hội bao gồm Sử – Địa – GDCD – Văn – ...
Th9
Chương trình Toán lớp 11: Nội dung các chuyên đề Toán lớp 11
Nội dung chương trình Toán lớp 11 gồm những gì? Bao gồm các chuyên đề ...
Th9
[2023] Hợp chất hữu cơ là gì? Tính chất, phân loại hợp chất hữu cơ
Hợp chất hữu cơ là gì? Khái niệm, tính chất và cấu tạo phân tử ...
Th9