Hình chóp tứ giác điều là hình chóp có đáy là hình vuông, các mặt bên là các tam giác cân. Chuyên đề khối chóp tứ giác đều là một trong những phần kiến thức quan trọng của phần hình học lớp 12. Việc nắm vững được lý thuyết, công thức và bài tập thể tích khối chóp tứ giác đều sẽ giúp các bạn đạt được điểm cao môn toán, chinh phục được mục tiêu mình đặt ra.
Nếu bạn đang loay hoay với “mớ” hỗn độn về chuyên đề kiến thức này thì cũng đừng quá lo lắng. Gia sư Thành Tâm sẽ lần lượt hướng dẫn và trả lời các thắc mắc xoay quanh chuyên đề khối chóp đều một cách dễ hiểu nhất. Hãy cùng đọc và tham khảo nhé!
Tính chất của hình chóp tứ giác đều
Hình chóp tứ giác đều có các tính chất sau:
- Đáy là hình vuông.
- Các cạnh bên bằng nhau.
- Tất cả các mặt bên là các tam giác cân bằng nhau.
- Chân đường cao trùng với tâm mặt đáy (Tâm mặt đáy là giao điểm của 2 đường chéo).
- Tất cả các góc tạo bởi cạnh bên và mặt đáy bằng nhau.
Ví dụ: Cho hình chóp tứ giác đều S.ABCD thì:
→ Tứ giác ABCD là hình vuông có tâm O.
→ SO vuông góc với mặt phẳng (ABCD).
→ Cạnh SA = SB = SC = SD
→ Góc (SA; (ABCD)) = góc (SB; (ABCD)) = góc (SC; (ABCD)) = góc (SD; (ABCD)).
Công thức tính thể tích khối chóp tứ giác đều
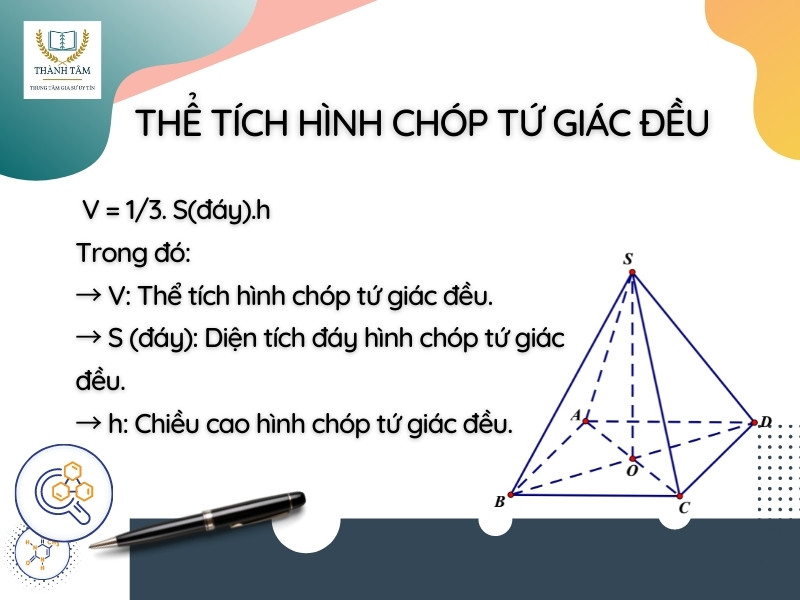
Công thức tính thể tích khối chóp tứ giác đều: V = 1/3. S(đáy).h
Trong đó:
→ V: Thể tích hình chóp tứ giác đều.
→ S(đáy): Diện tích đáy hình chóp tứ giác đều.
→ h: Chiều cao hình chóp tứ giác đều.
[Hướng dẫn] Cách tính thể tích hình chóp tứ giác đều
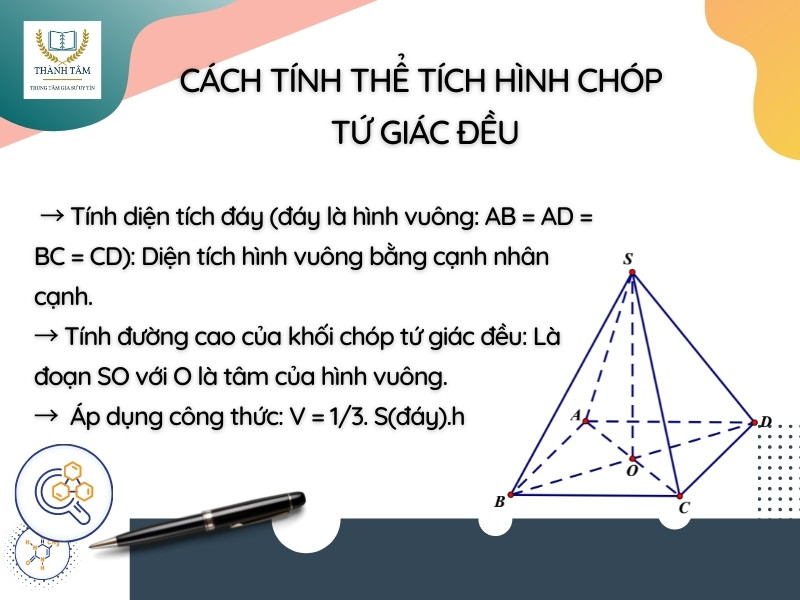
Các dạng toán tính thể tích của một khối chóp tứ giác đều thường khá đa dạng. Tuy nhiên, khi các bạn nắm được bản chất của vấn đề thì mọi dạng toán các bạn điều có thể làm được. Tóm lại, để tính được thể tích của khối chóp tứ giác đều, chúng ta phải:
→ Tính diện tích đáy (đáy là hình vuông: AB = AD = BC = CD): Diện tích hình vuông bằng cạnh nhân cạnh.
→ Tính đường cao của khối chóp tứ giác đều: Là đoạn SO với O là tâm của hình vuông.
Ví dụ: Cho hình chóp tứ giác đều S.ABCD, có độ dài cạnh đáy là a, độ dài cạnh bên là 2a. Tính thể tích khối chóp đều.
Hướng dẫn:
→ Diện tích đáy ABCD: S = AB.AD = a.a = a²
→ Gọi O là tâm của đáy ABCD. Theo tính chất của hình chóp tứ giác đều, suy ra: SO là chiều cao.
→ Độ dài SO² = SA² – OA² = (2a)² – (a/2)² = 15a²/4 → AO= a√15/2
→ Thể tích hình chóp S.ABCD = 1/3.S.h = 1/3.a². a√15/2 = a³√15/6
[Chuyên đề] bài tập tính thể tích khối chóp tứ giác đều
Dưới đây là một số dạng bài tập có hướng dẫn chi tiết về chuyên đề thể tích hình chóp tứ giác đều. Các bạn có thể tham khảo nhé!
>>> Xem thêm: [Tư Vấn] Tìm gia sư dạy Toán lớp 12, luyện thi đại học TPHCM
Kinh nghiệm làm bài thể tích hình chóp tứ giác, tam giác đều
Thật ra, với mỗi tiết toán với thời gian 45 phút, giáo viên bộ môn sẽ không thể nào giảng bài tỉ mỉ tất cả lý thuyết và bài tập. Thầy cô giáo sẽ hướng dẫn kiến thức cơ bản nhất, kiến thức ngoài sách giáo khoa thì con trẻ phải tự tìm hiểu. Do vậy, các con phải:
- Phân loại và làm bài tập thật nhiều. Điều này giúp chúng ta hiểu sơ bộ và bản thân sẽ có những thắc mắc. Và khi đến tiết học, thầy cô giáo giảng bài mình sẽ dễ hiểu hơn, hỏi thầy cô những điều chưa rõ.
- Không biết không hiểu thì phải hỏi thầy cô hay bạn bè. Đừng bao giờ giấu điều mà mình không biết, biết đâu nó sẽ xuất hiện trong bài kiểm tra hay bài thi THPT thì sao.
- Học toán là đòi hỏi tư duy tính toán chứ không phải là học vặt, học dồn cho lấy có.
- Nhớ chính xác công thức và đổi đồng nhất đơn vị đo độ dài cạnh.
- Bấm máy tính không những phải chính xác mà còn phải nhanh, đúng đáp án.
KẾT LUẬN
Gia sư Thành Tâm hi vọng qua bài viết này, các bạn sẽ lần lượt giải đáp được những thắc mắc của mình về chuyên đề công thức và các dạng bài tập tính thể tích hình chóp tứ giác đều. Mỗi chuyên đề kiến thức trong chương trình toán lớp 12 điều “có mặt” trong đề thi THPT. Kiến thức mới thì luôn khó, muốn đạt được điểm cao thì phải nổ lực và cố gắng nắm vững kiến thức nhé.
>>> Xem thêm: [Tổng hợp] Công thức Hình Học lớp 12 “bức phá” kỳ thi THPT

Gia Sư Đà Nẵng: [Tư Vấn] Tìm Gia Sư Các Môn từ lớp 1-12!
Chi nhánh gia sư Đà Nẵng của Thành Tâm đã hoạt động hơn 6 năm, ...
Th11
[Chuẩn] Cách Học Tốt Môn Lịch Sử Lớp 12 Để Ôn Thi THPT
Môn Lịch Sử là một trong 3 môn xã hội được quy định trong kì ...
Th10
Kinh Nghiệm, Nội Dung Kiến Thức Ôn Thi Vào Lớp 10 Môn Văn 2023
Toán – Văn – Anh là bộ ba môn học mà Bộ GD-ĐT lựa chọn ...
Th10
Chia Đa Thức Cho Đơn Thức Lớp 8: Lý Thuyết & Bài Tập!
Chia đa thức cho đơn thức nằm ở phần chương 1 toán đại số của ...
Th10
[Tóm Tắt A-Z] Chương Trình Toán Lớp 10- Gia Sư Thành Tâm
Chương trình toán lớp 10 gồm những chuyên đề nào? Số lượng bài và tổng ...
Th9
[Đầy Đủ] Phương pháp luyện thi THPT quốc gia tổ hợp môn xã hội
Tổ hợp môn xã hội bao gồm Sử – Địa – GDCD – Văn – ...
Th9
Chương trình Toán lớp 11: Nội dung các chuyên đề Toán lớp 11
Nội dung chương trình Toán lớp 11 gồm những gì? Bao gồm các chuyên đề ...
Th9
[2023] Hợp chất hữu cơ là gì? Tính chất, phân loại hợp chất hữu cơ
Hợp chất hữu cơ là gì? Khái niệm, tính chất và cấu tạo phân tử ...
Th9